
Calculus Volume Integral Mathematics Stack Exchange
Experts are tested by Chegg as specialists in their subject area $\begingroup$ @saulspatz Well we want to find the SURFACE area of part of the paraboloid that lies above the plane z = 4 And there is a formula to calculating surface area as shown in my first picture $\endgroup$ – Not Friedrich gauss Apr 5 ' at 426
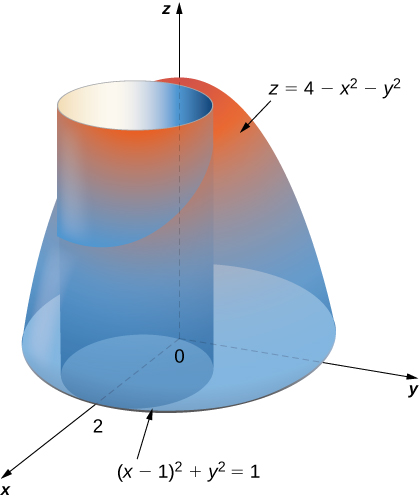
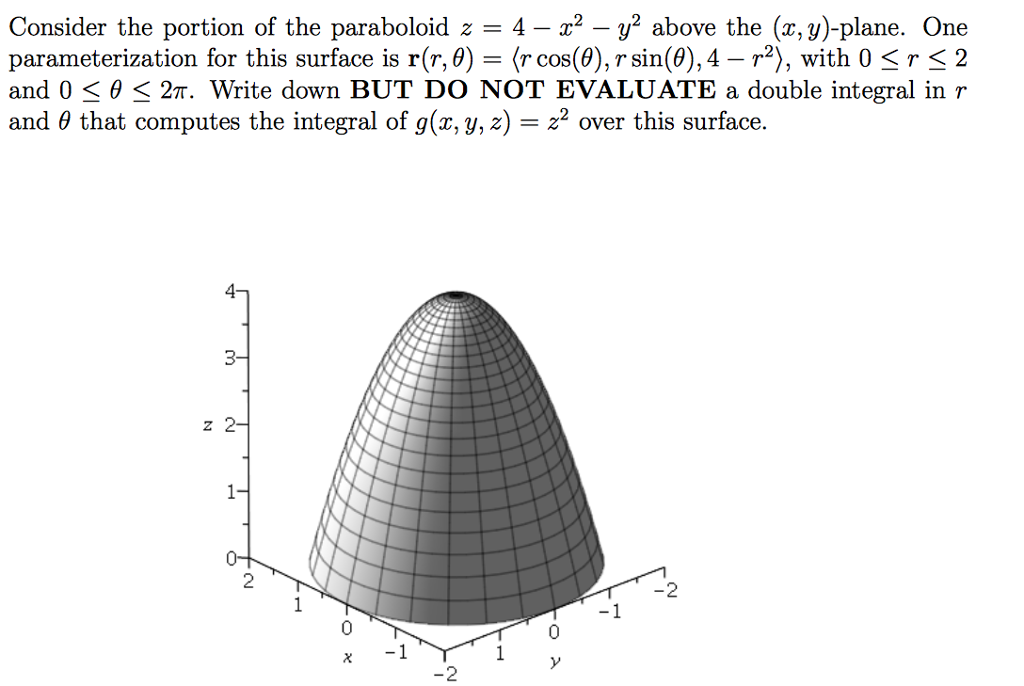
S is the part of the paraboloid z=4-x^2-y^2
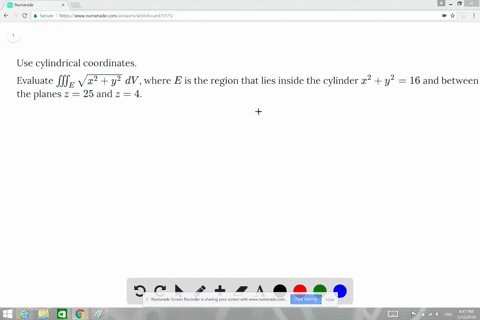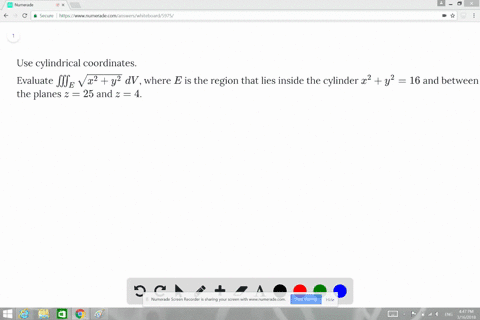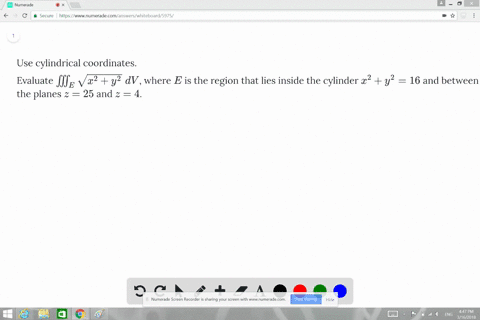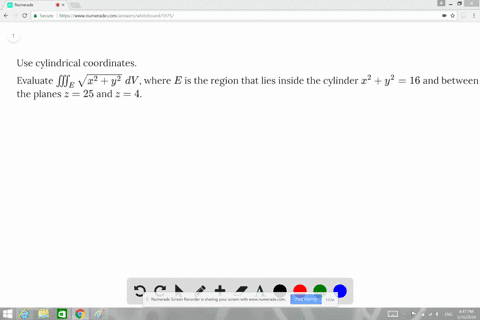
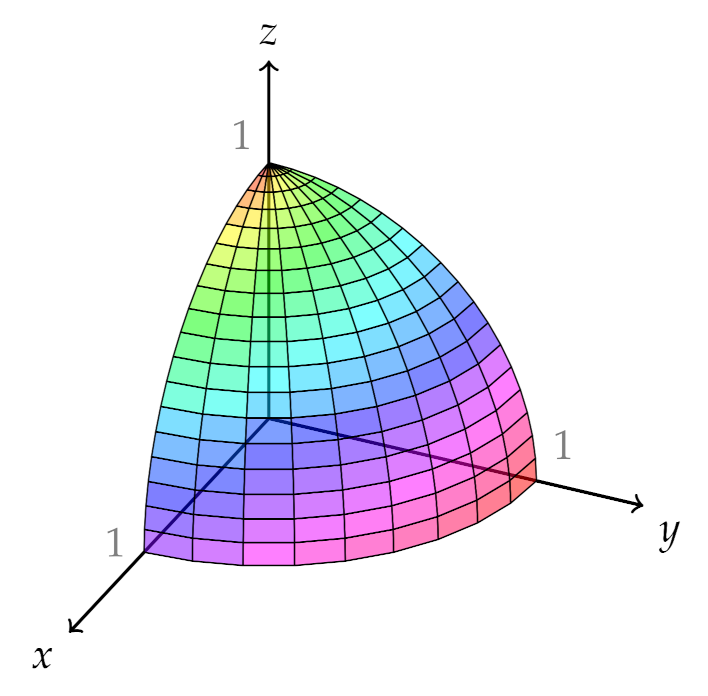
S is the part of the paraboloid z=4-x^2-y^2-Please ask as separate question(s) if any of these are not already established Concept of partial derivatives The area of a surface, f(x,y), above a region R of the XYplane is given by int int_R sqrt((f_x')^2 (f_y')^2 1) dx dy where f_x' and f_y' are the partial derivatives of f(x,y) with respect to x and y respectively In converting the integral of aFind an equation for the paraboloid z = 4−(x2y2) z = 4 − ( x 2 y 2) in cylindrical coordinates (Type theta in your answer) Cylindrical Coordinates In many practical situations, using a

16 Vector Calculus Copyright Cengage Learning All Rights
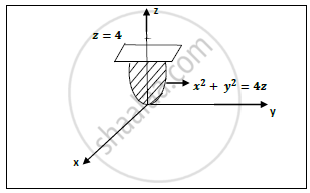
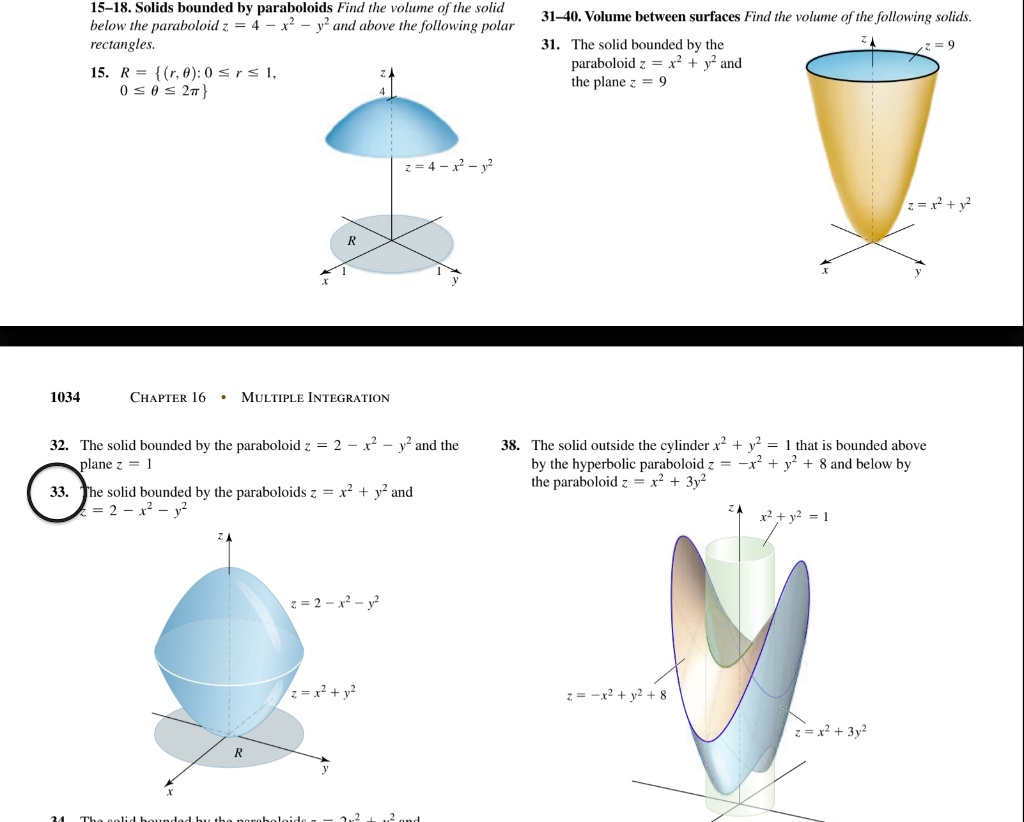
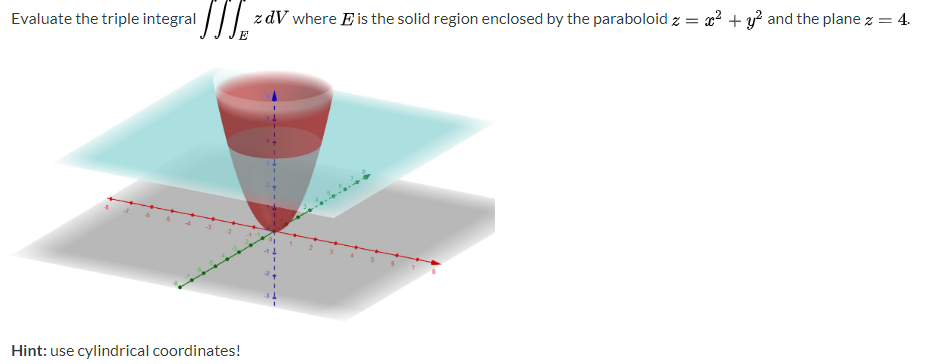
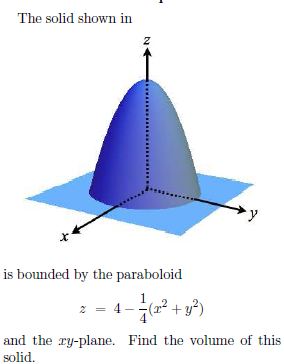
Paraboloid z = x^2 4*y^2 Parameterized as a graph The picture only includes portions of the parameterized surface with z plot3d(r,s,r^24*s^2,r=22,s=11,view=22,11,04,axes=framed,shading=zhue);Find stepbystep Calculus solutions and your answer to the following textbook question At what point on the paraboloid $$ y = x^2z^2 $$ is the tangent2 Let T be the solid bounded by the paraboloid z= 4 x2 y2 and below by the xyplane Find the volume of T (Hint, use polar coordinates) Answer The intersection of z= 4 2x 22y and xyplane is 0 = 4 x2 y;ie x2 y = 4 In polar coordinates, z= 4 x2 y 2is z= 4 rSo, the volume is Z Z 4 x2 y2dxdy = Z 2ˇ 0 Z 2 0 4 r2 rdrd = 2ˇ Z 2 0 4r r3 2 dr
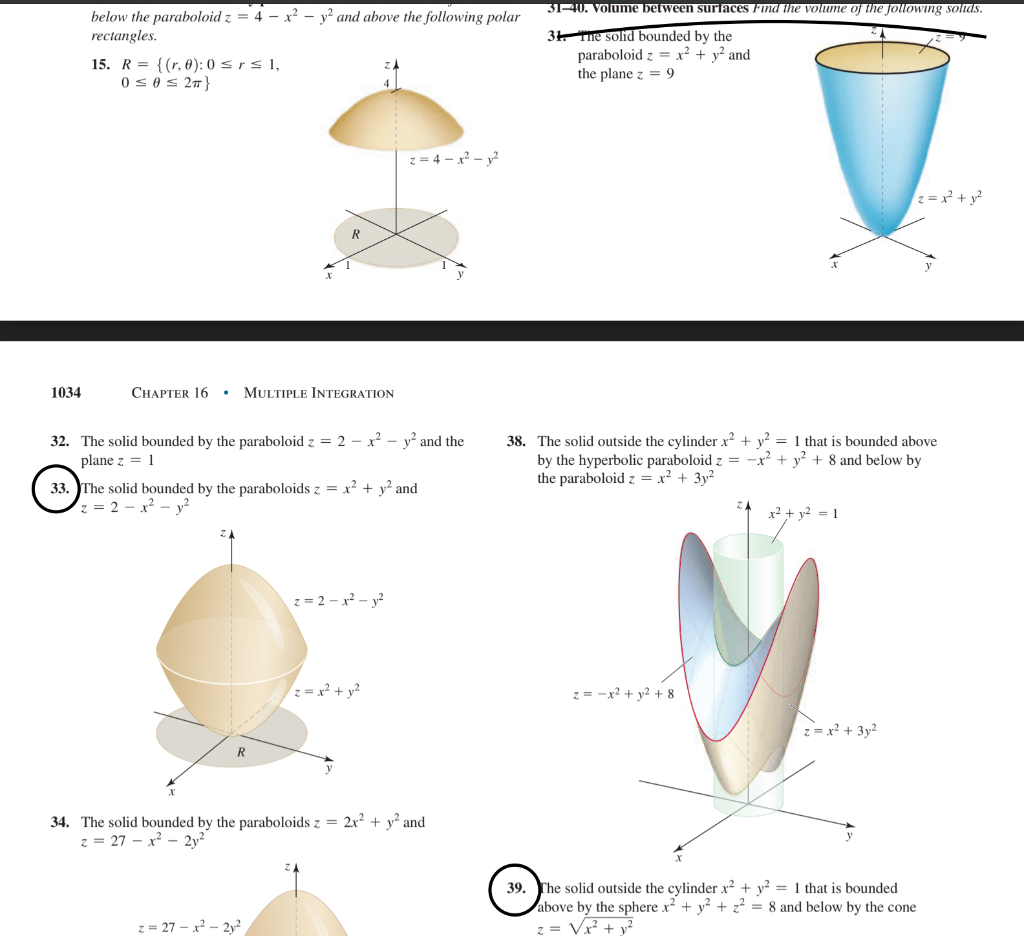
I assume the following knowledge;We will assume that the paraboloid they were trying to write is {eq}\begin{align*} z &= 2x^2 2y^2 \\ &= 2 ( x^2 y^2) \end{align*} {/eq} This is a paraboloid Anyway, all that we needed toDownload scientific diagram A hyperbolic paraboloid z = x 2 − y 2 from publication Polyhedral sculptures with hyperbolic paraboloids This paper describes the results of our experiments
S is the part of the paraboloid z=4-x^2-y^2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 | ||
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
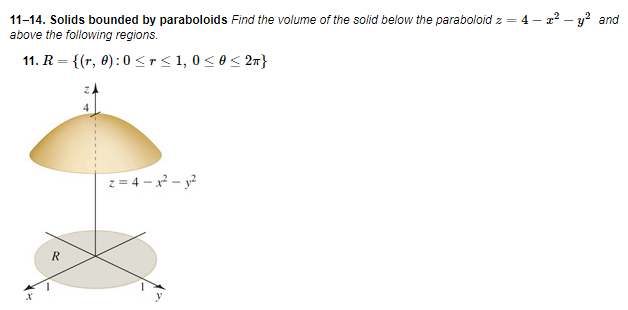 |  |  |
 | ||
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「S is the part of the paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
First draw the base region R in the xy plane It is a triangle in the first quadrant Label the corners which are (0,0) (0,2) and (2,2) Next try to draw the paraboloid in the xyz plane It doesn't have to be perfect But we see it passes through (0,0,0) Holding x=0, it intersects the yz plane with a parabola opening upward z=4y^2 Now, the limits of integration in x and y When you graphed it you probably saw that the paraboloid and plane intersect where z= 4 and itex4(4)= 16= x^2 y^2/itex which, projected to the xyplane is the circle itexx^2 y^2= 16/itex and the entire figure is inside that cylinder
Incoming Term: paraboloid z=4-x^2-y^2, s is the part of the paraboloid z=4-x^2-y^2, find the volume of the solid below the paraboloid z=4-x^2-y^2, find the surface area of the part of the paraboloid z=4-x^2-y^2,




0 件のコメント:
コメントを投稿