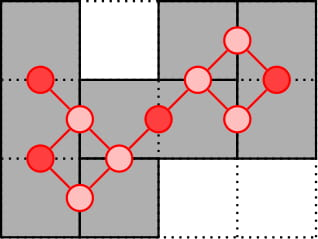
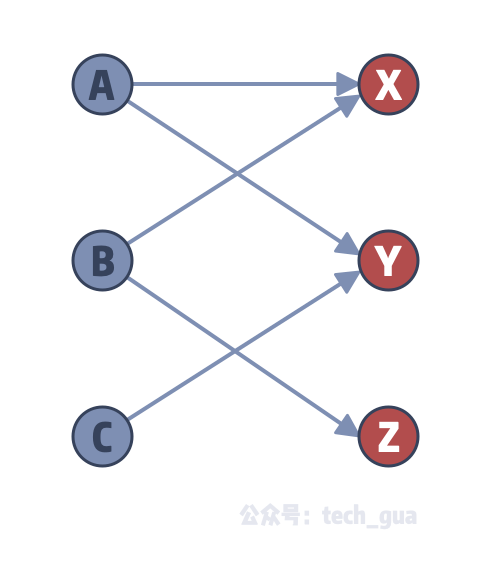
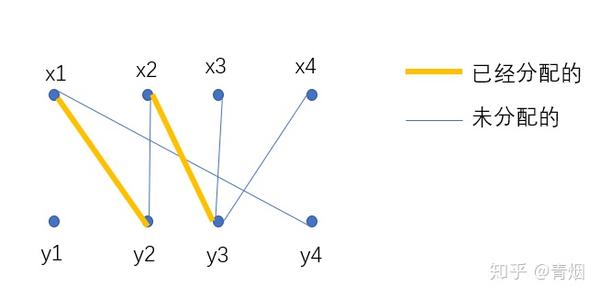
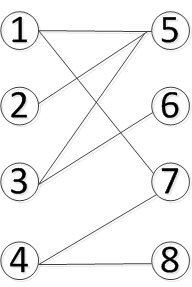
图5 KM算法的第三步 继续为x4匹配,发现已经没有了增广路了,已经达到了本次匈牙利算法所能找到的最大匹配,但是我们的最佳匹配还没有完成,因此我们需要更新顶标,首先我们求解d,此时我们在 遍历的点为{x1,x2,x3,x4},在 中遍历的点为{y2,y3,y4},从而我们求得d = 1,更新如下:KM算法是一种 计算机算法 ,功能是求完备匹配下的最大权 匹配 。 在一个 二分图 内,左顶点为X,右顶点为Y,现对于每组左右连接XiYj有权wij,求一种匹配使得所有wij的和最大。 中文名 KM算法 用 途 求的是完备匹配下的最大权匹配 基本原理 相等子图等 注 意 861 二分图的最大匹配 时间复杂度 没有任何一个点在多条边上,称为一个匹配。 虽然是无向图,但是存边存的是有向边,算法是只看左边的情况。所以只需要存左边指向右边就可以了。
匹配算法 Daltao S Blog
二分图最大匹配算法
二分图最大匹配算法-二分图 定义¶ 二分图,又称二部图,英文名叫 Bipartite graph。 二分图是什么?节点由两个集合组成,且两个集合内部没有边的图。 换言之,存在一种方案,将节点划分成满足以上性质的两个集合。 性质¶ 二分图: 二分图是一个无向图,点集分成子集x和y,图中每一条边都是一边在x一边在y 当且仅当无向图g的每一个回路次数都是偶数时(包括0),g就是一个二分图 匹配 介绍完二分图后我们看看匹配 匹配:如果任意两个边的端点都不相同,我们就称之为匹配。




二分图最大匹配的可行边和必须边 躲不过这哀伤的博客 程序员信息网 程序员信息网
二分图匹配 基本概念: 给定一个二分图g,在g的一个子图m中,m的边集{e}中的任意两条边都不依附于同一个顶点,则称m是一个匹配。 通常分为以下几种匹配: 一、 最大匹配 指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。二分图最大匹配及其应用 二分图与图的匹配 例 1 t he p erfect s tall 题目来源:usaco, poj1274 农夫john的牛棚共有m个牛栏,其中一共 养了n头奶牛。每头奶牛只愿意在它喜欢 的那些牛栏中产奶。一个牛栏只能容纳一 头奶牛,一头奶牛也只在一个牛栏中产奶。 对已经连好的图求最大匹配数 最小路径覆盖数=顶点数n最大匹配数 Nkoj 1684 1465 1681 1070 courses Taxi Cab Scheme Girls and boys 信和信封的问题 poj 2239 1422 1325 1719 2594 Selecting Courses Air Raid 最小路径覆盖 Machine Schedule Shooting Contest Treasure Exploration 2195 Going Home带权二分图(km算法
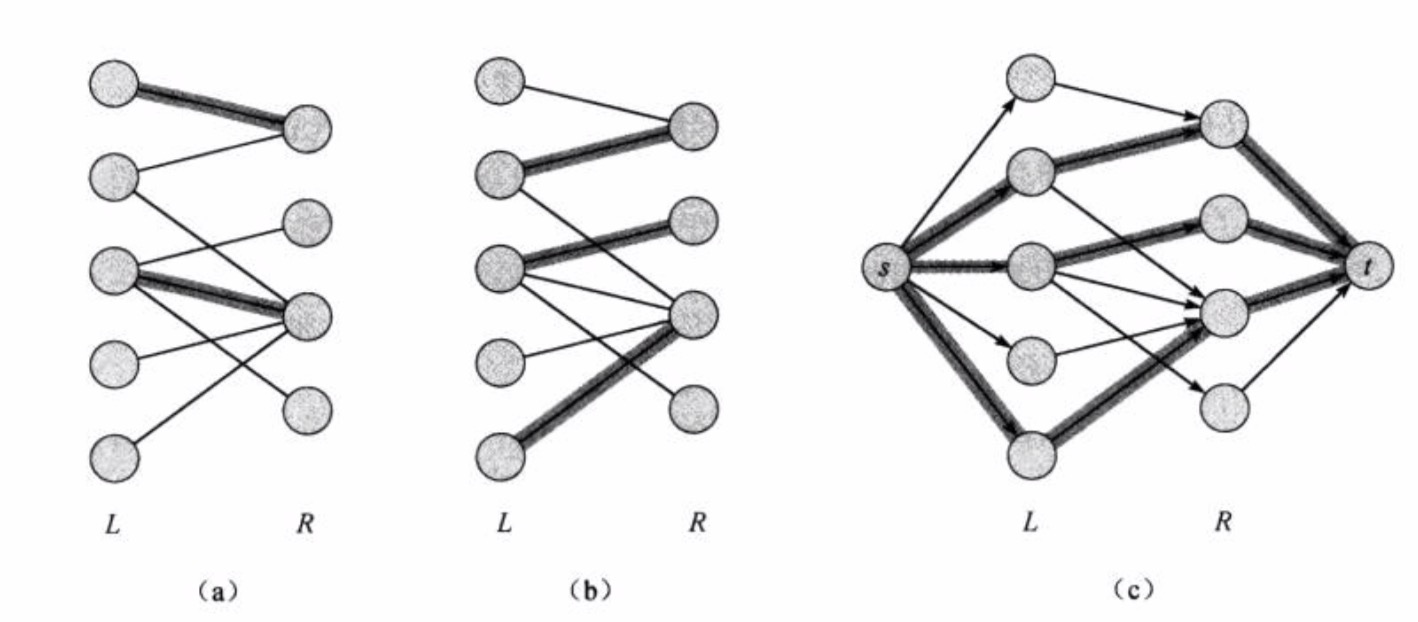
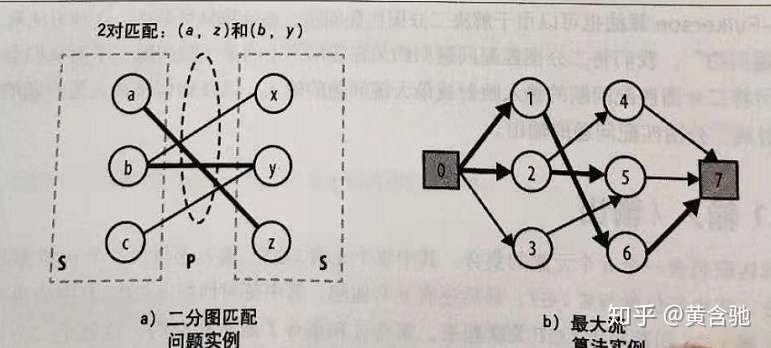
二分图最大匹配总结 1。 一个二分图中的最大匹配数等于这个图中的最小点覆盖数 本文将是这一系列里最短的一篇,因为我只打算把König定理证了,其它的废话一概没有。 1 什么是二分图; 2 什么是二分图的匹配;/* 匈牙利算法邻接表形式 使用前用init()进行初始化,给uN赋值 加边使用函数addedge(u,v) */ const int MAXN=5010;//点数的最大值 const 这节课介绍无权二部图中的最大匹配问题 MaximumCardinality Bipartite Matching (MCBM)。匹配 (Matching) 的意思是一些边的集合,这些边不能有共同的节点。MCBM 要求寻找一组满足要求的边,使得边的数量最大化。可以将 MCBM 规约到最大流问题,用 EdmondsKarp 或者 Dinic 等最大流算法求解。
二分图的最大匹配、完美匹配和匈牙利算法Algorithms二分图匹配, 图论, 算法这篇文章讲无权二分图(unweighted bipartite graph)的最大匹配(maximum matching)和完美匹配(perfect matching),以及用于求解匹配的匈牙利算法(Hungarian Algorithm);不讲带权二分图的最佳匹配。 完备匹配的条件没有完美匹配那么严苛,它要求一个匹配中包含二分图中某个集合的全部顶点。比如,x 集合中的顶点都有匹配边。 匈牙利算法就是要找出一个图的最大匹配。 算法思想 其实匈牙利算法如果要感性理解起来是很容易的,核心就在于 冲突和协调 匈牙利算法是基于Hall定理中充分性证明的思想,它是二分图匹配最常见的算法,该算法的核心就是寻找增广路径,它是一种用增广路径求二分图最大匹配的算法。 二分图 二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割




算法导论 之 图 不带权二分图最大匹配 匈牙利算法 的技术博客 51cto博客



干货 二分图详解 知乎
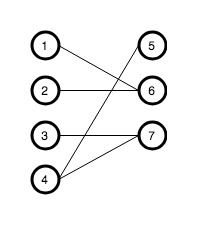
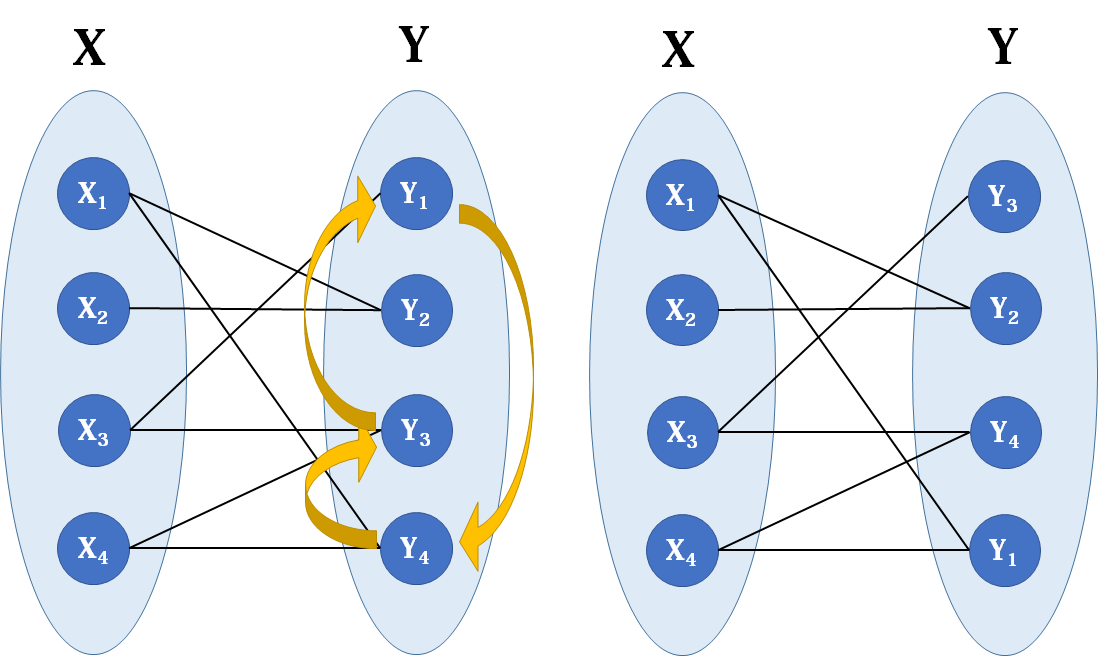
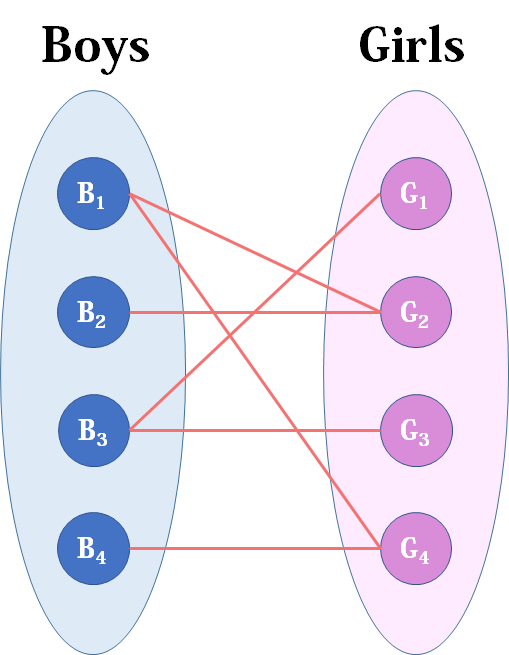
图 4 是一个最大匹配,它包含 4 条匹配边。 匈牙利算法解决的问题背景:如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在,你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。 本着救人一命,胜造七级浮屠的原则,你想要尽给定一个二分图,其左部点的个数为 $n$,右部点的个数为 $m$,边数为 $e$,求其最大匹配的边数。 左部点从 $1$ 至 $n$ 编号二分图最大匹配: 给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)。 首先我们先了解两个概念




二分图匹配及匈牙利算法的全面讲解及python实现




二分图匹配 匈牙利算法原理与实现 简书
KM算法(二分图的最佳完美匹配) (1)初始化Lx数组为该boy的一条权值最大的出边。 初始化Ly数组为 0。 (2)对于每个boy,用DFS为其找到一个girl对象,顺路记录下S和T集,并更新每个girl的slack值。 若不能为其找到对象,则转3。 (3)找出非T集合的girl的最小 算法导论——二分图最大匹配 二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。2 days ago 策略算法工程师之路图优化算法(一)(二分图&最小费用最大流 目录1图的基本定义2双边匹配问题21 二分图基本概念22 二分图最大匹配求解23 二分图最优匹配求解24 二分图最优匹配建模实例241 二分图最优匹配在师生匹配中 ,Unity开发者联盟大宇光环科技



今際の国の呵呵君 Algorithm Maximum Matching Of Bipartite Graph 二分图的最大匹配



最大二分匹配与匈牙利算法 吾青
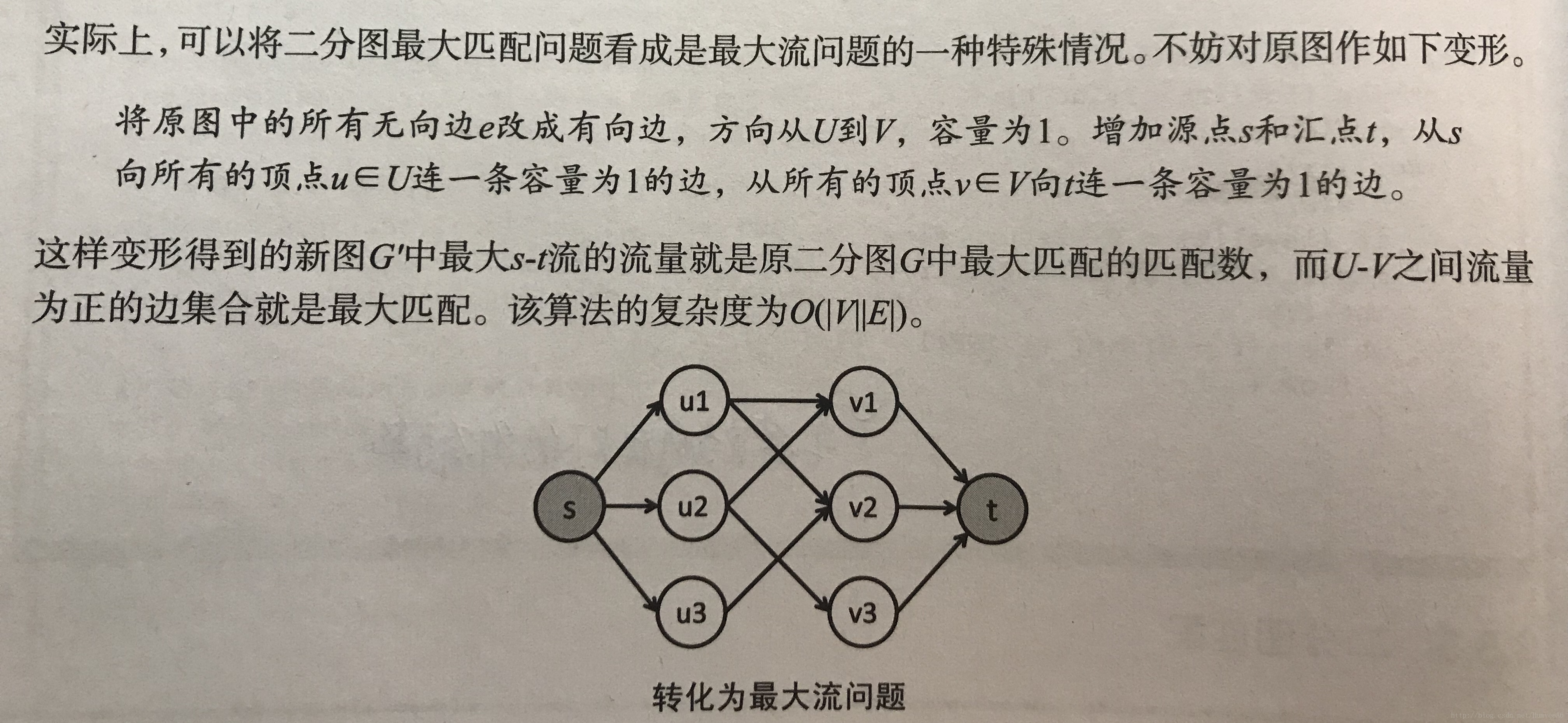
二分图的概念:二分图是图中的一种特殊模型,如果图的顶点v可以分割成两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则该图G成为一个二分图。二分图如下:本文通过一个问题来引出二分图的最大匹配算法 。这篇将 二分图最大匹配 转换成 最大流问题 的思维过程,想必会让你对图算法又了新的认识。 算法题目的考察从广义上来讲,就是在考察你 是否能将这个问题对应到一个你熟悉的求解模型和方法上 ,如果你抽象得当,你就可以利用已有的算法,去高效的求解30 % 30\% 30% 的数据,满足 n ≤ 100 n\leq 100 n ≤ 100 。 对于 60 % 60\% 60% 的数据,满足 n ≤ 500 n\leq 500 n ≤ 500 ,且保证数据随机 。



二分图匹配和匈牙利算法 简书




二分图匹配 匈牙利算法 程序员大本营
二分图的带权匹配就是求出一个匹配集合,使得集合中边的权值之和最大或最小。 而二分图的最佳匹配则一定为 完备匹配 ,在此基础上,才要求匹配的边权值之和最大或最小。 二分图的 带权匹配与最佳匹配不等价,也不互相包含 。 我们可以使用KM算法实现Heoi12朋友圈 二分图匹配 二分图最大匹配 4星 未练习 010 heoi13钙铁锌硒维生素 二分图匹配 高斯消元 4星 未练习 104 hnoi13消毒 二分图匹配 二分图最大权匹配 dfs 3星 未练习 109 hnoi14画框 分治 二分图匹配 最小生成树 二分图最大权匹配 3星 未 在二分图最大匹配中,每个点(不管是X方点还是Y方点)最多只能和一条匹配边相关联,然而,我们经常遇到这种问题,即二分图匹配中一个点可以和多条匹配边相关联,但有上限,或者说,L i 表示点i最多可以和多少条匹配边相关联。 二分图多重匹配分为二分图多重最大匹配与二分图多重最




Ppt 二分图匹配powerpoint Presentation Free Download Id




二分图最大匹配的一些证明 Five的技术博客 51cto博客
§1图论点、边集和二分图的相关概念和性质 php §2二分图最大匹配求解 html 匈牙利算法、HopcroftKarp算法 node §3二分图最小覆盖集和最大独立集的构造 ios §4二分图最小路径覆盖求解 算法 §5二分图带权最优匹配求解 数据结构 KuhnMunkers算法 闭包 §6小结 less 每章节都详细地讲解了问题介绍,算法原理 最大匹配 一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。 图 4 是一个最大匹配,它包含 4 条匹配边。 匈牙利算法解决的问题背景:如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在,你拥有的大概就是下面这样一张二分图匹配 本页面部分定义引自本科同学renfei的个人博客。 问题(最大二分匹配) 给定二分图,求解其最大匹配的匹配边数 二分图 二分图 G=(V,E) 是一个无向图,其顶点集 V 可分解为两个互不相交的子集 A, B ,对 \forall e=(a, b) \in E 有 a \in A, b \in B 匹配




通俗易懂小白入门 二分图最大匹配 匈牙利算法
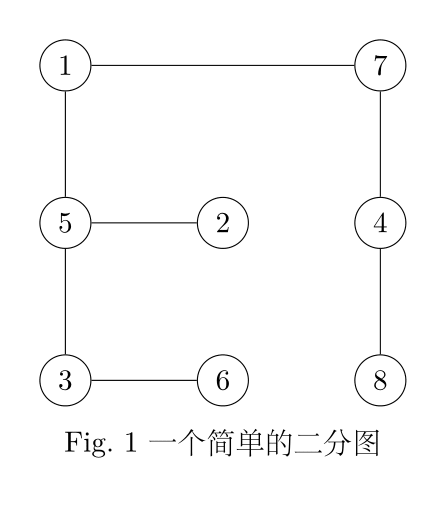



二分图最大匹配问题与匈牙利算法的核心思想 始终
二分图的最大匹配、完美匹配和匈牙利算法 这篇文章讲无权二分图(unweighted bipartite graph)的最大匹配(maximum matching)和完美匹配(perfect matching),以及用于求解匹配的匈牙利算法(Hungarian Algorithm);不讲带权二分图的最佳匹配。 二分图 :简单来说,如果二分图的 带权匹配与最优匹配不等价,也不互相包含 。 以下是一些转换的思路: KM算法是求最大权完备匹配,如果要求最小权完备匹配怎么办? 方法很简单,只需将所有的边权值取其相反数,求最大权完备匹配,匹配的值再取相反数即可。 KM算法的运行 最小边覆盖 = 最大独立集 = V 最大匹配数 这个是在原图是二分图上进行的 最小路径覆盖和最小边覆盖不同,不要求给的图是二分图,而是要求是N x N的有向图,不能有环,然后根据原图构造二分图,构造方法是将点一分为二,如,i分为i1和i2然后如果i和j有边,那么就在i1和j2之间连一条边。
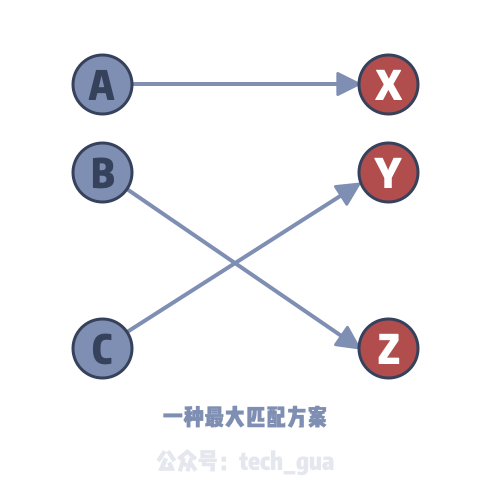



二分匹配的最大流思维 一瓜算法小册
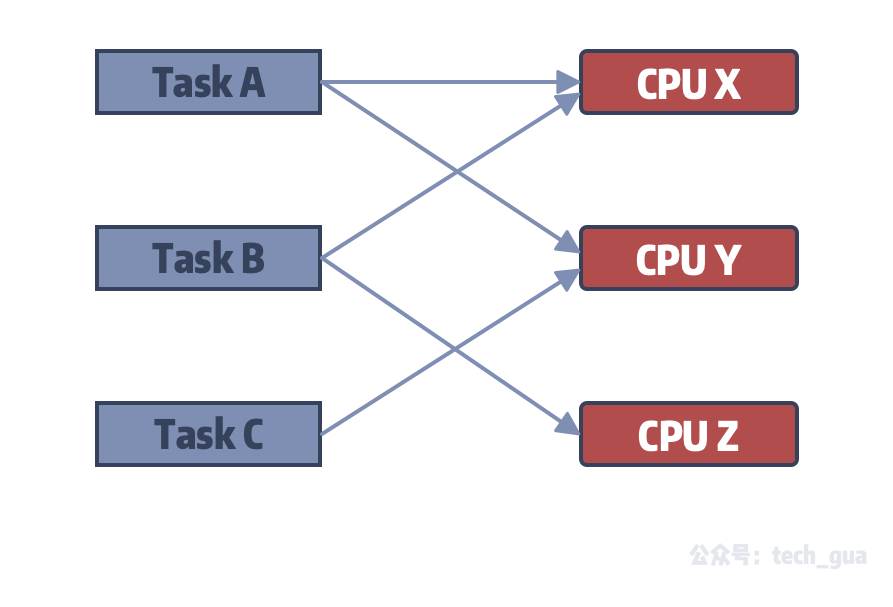



二分匹配的最大流思维 一瓜算法小册
二分图匹配及其应用 一个无向图g=(v,e)的匹配m是指g中若干条边的集合,在m中任意两条边都没有公共的端点。 在二分图中边数最多的匹配,称为二分图的最大匹配。 1 利用增广路径求二分图最大匹配——匈牙利算法
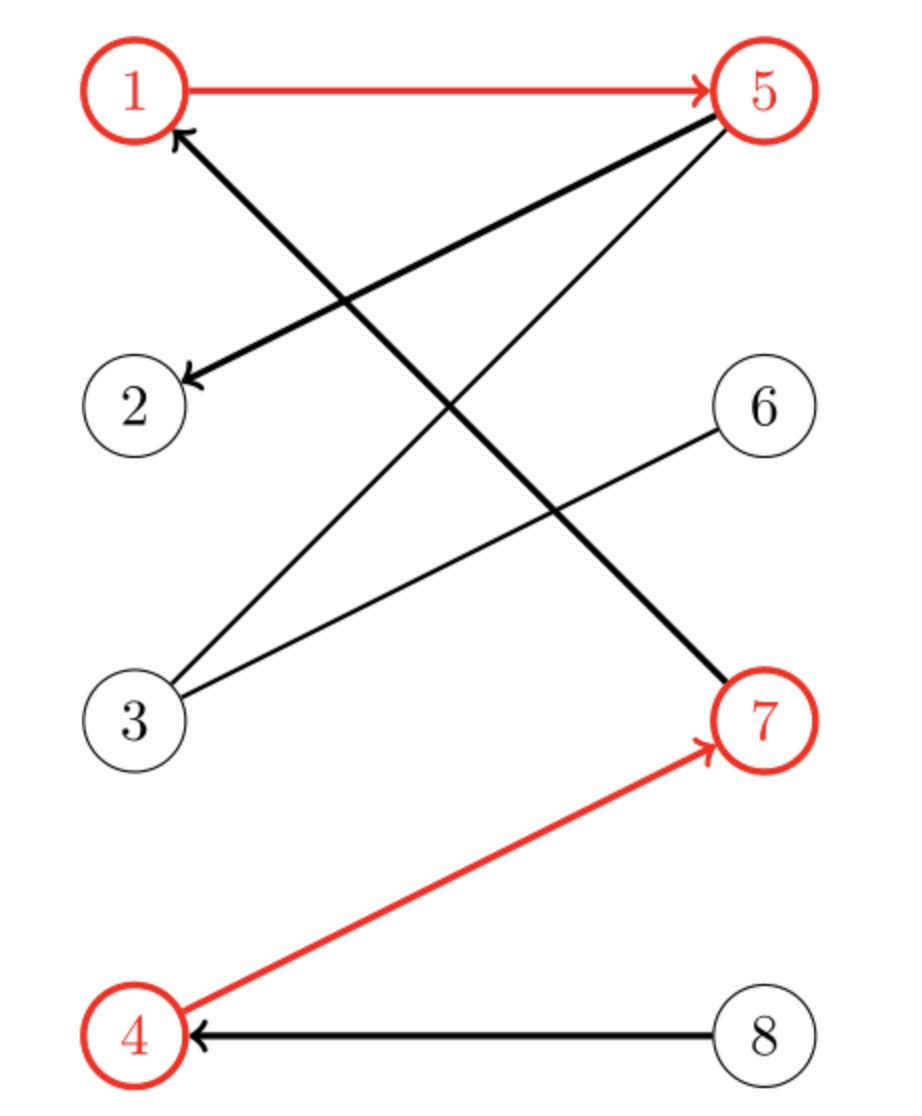



最大二分匹配与匈牙利算法 吾青




通俗易懂小白入门 二分图最大匹配 匈牙利算法



蒟蒻图论 二分图最大带权匹配 蒟蒻のblog
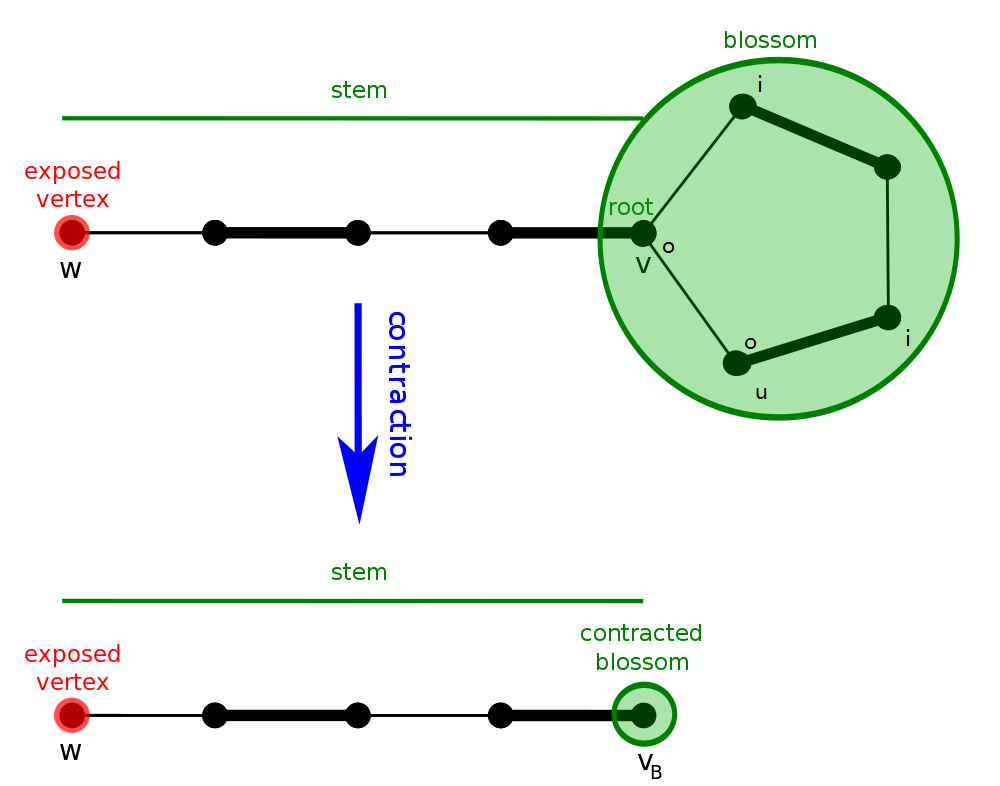



一般图最大匹配 Oi Wiki



Km算法详解 模板 二分图最大权值匹配 Shyoldman的博客 Csdn博客 二分图最大权值匹配



二分图匹配の匈牙利算法 银河渡舟



蒟蒻图论 二分图匹配 蒟蒻のblog




二分图最大匹配 匈牙利算法 我不吃饼干呀 博客园




Acwing 861 详解二分图模版1 染色法判断二分图2 匈牙利算法 Acwing




二分图 牛客博客
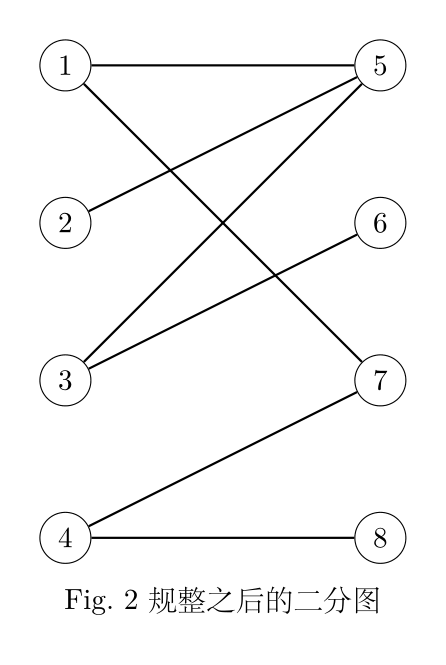



二分图最大匹配问题与匈牙利算法的核心思想 始终




用于二分图匹配的匈牙利算法 Comzyh的博客
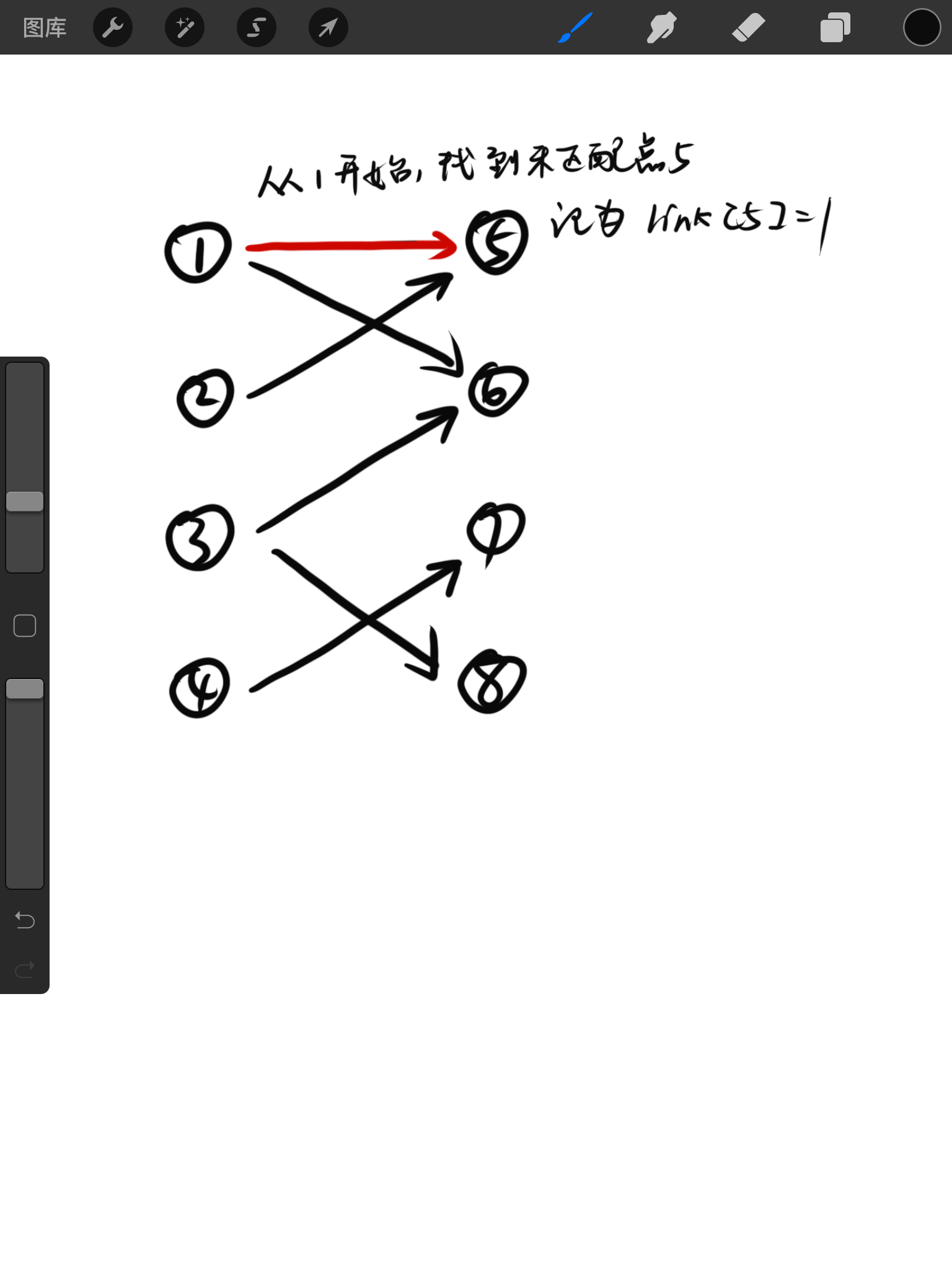



最大二分匹配与匈牙利算法 吾青



算法导论 二分图最大匹配 简书




求解分配问题 二 二分图最大匹配算法 Wangzhenyang2的博客 Csdn博客




通俗易懂小白入门 二分图最大匹配 匈牙利算法




二分图的最大匹配 完美匹配 匈牙利算法 转载 Mb6131cb1bd1974的技术博客 51cto博客




二分图最大匹配 匈牙利算法 整理 Sxh的博客 程序员宝宝 程序员宝宝
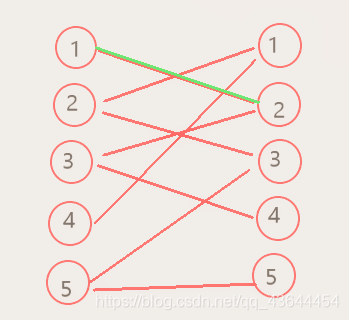



二分图判定 二分图匹配 匈牙利算法 多重匹配 最小顶点覆盖 带权二分图匹配 Km算法 Wa的一声就哭了 程序员秘密 程序员秘密



蒟蒻图论 二分图匹配 蒟蒻のblog




Python成神之路 二分匹配大总结 Bipartite Graph Matchings Lnjjf
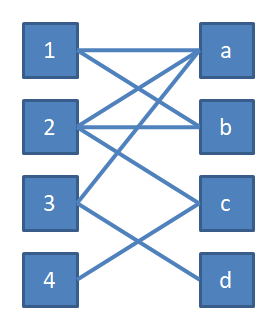



二分图相关算法 匈牙利算法学习笔记 Whatss7 博客园



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog




二分图匹配之最佳匹配 Km算法 Lanly 博客园




匹配算法 Daltao S Blog
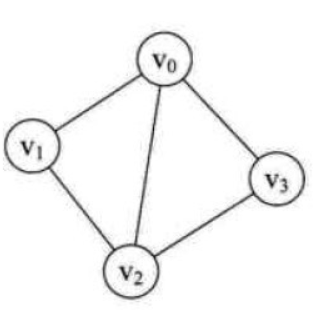



匈牙利匹配和最大权值匹配算法 Silence Cho 博客园



二分图最大匹配 匈牙利算法 洛谷p71座位安排 哔哩哔哩 Bilibili
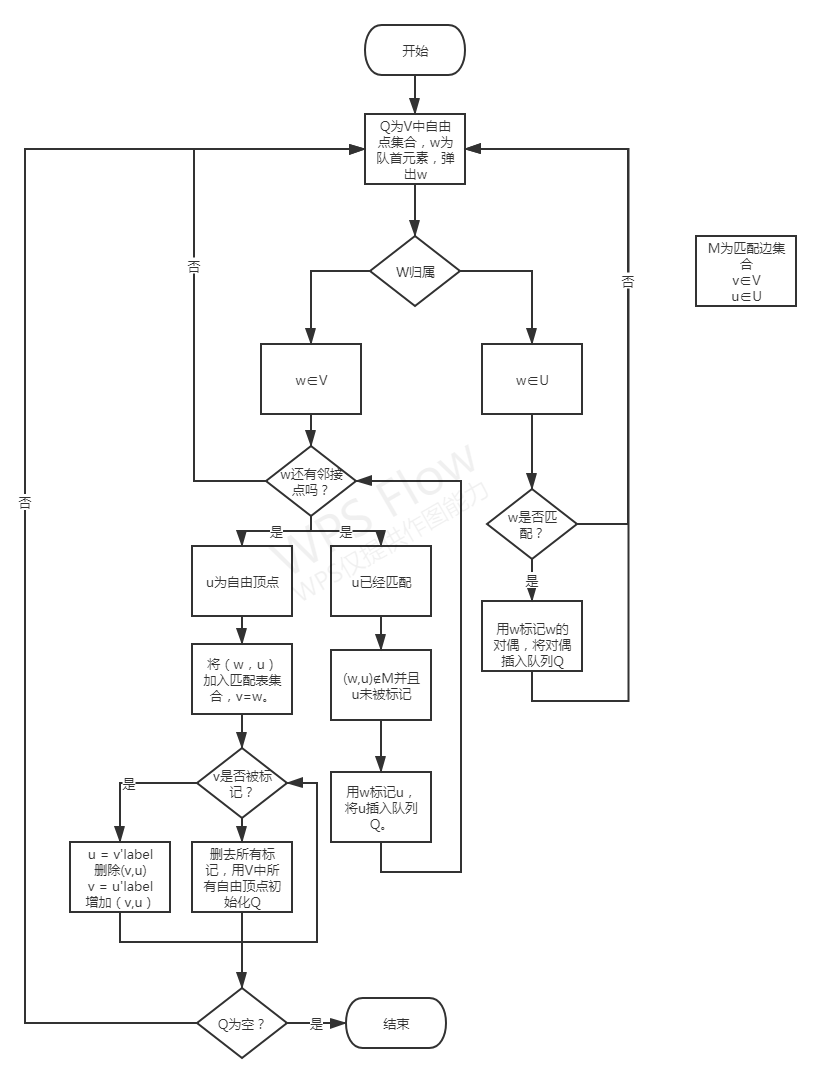



二分图最大匹配算法流程图 Zhouyupeng1016的博客 程序员宝宝 程序员宝宝
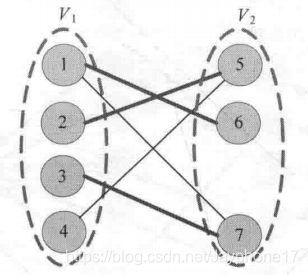



图论 入门级二分图最大匹配bipartite Matching Jayphone17的博客 Csdn博客 Bipartite Matching




二分图最大匹配的可行边和必须边 躲不过这哀伤的博客 程序员信息网 程序员信息网



模板 二分图最大匹配 最大流算法 Humveea6的博客 程序员宝宝 程序员宝宝



二分图的最大匹配 完美匹配和匈牙利算法 Yuanda S Blog
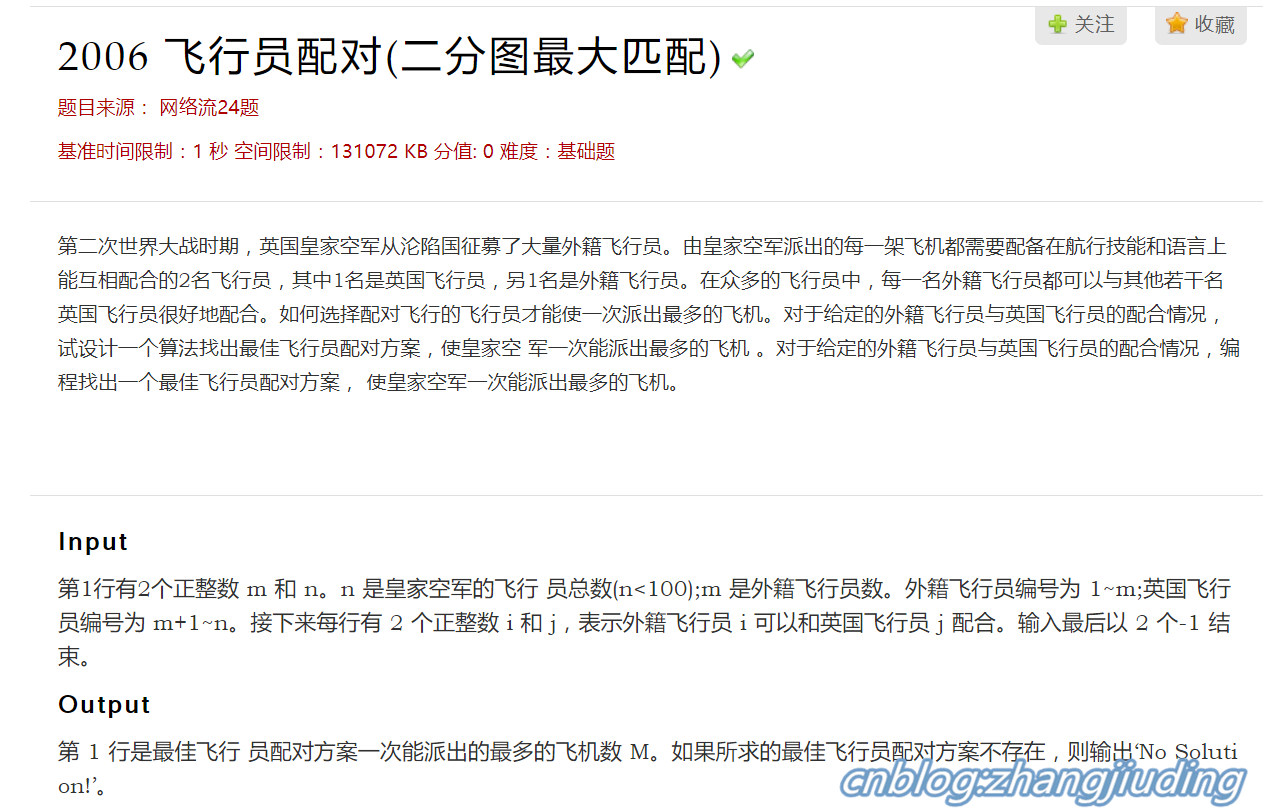



51nod 06 飞行员配对 二分图最大匹配 裸匈牙利算法求二分图最大匹配题 Ninding 博客园



二分图匹配与应用 哔哩哔哩 つロ干杯 Bilibili




二分图最大匹配的一些证明 Five的技术博客 51cto博客



算法学习笔记 5 匈牙利算法 知乎




二分图匹配 最大匹配 匈牙利算法 摸鱼世界 摸鱼酱的个人博客



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog




二分图匹配 指派问题 Herongwei 的blog Csdn博客
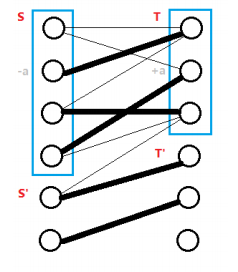



二分图最大权匹配 Oi Wiki



二分匹配的最大流思维 一瓜算法小册




二分图的最大匹配 匈牙利算法 简书



二分图最大权值匹配算法 Km算法 和匈牙利算法 知乎



网络流算法学习笔记2 简洁易懂 二分图匹配求解算法 代码及算法设计一书关于二分图匹配章节的翻译 知乎



二分图多重最大匹配 简书



二分图带权匹配km算法与费用流模型建立




二分图匹配 Ppt Download



二分图的最大匹配 完美匹配和匈牙利算法 Yuanda S Blog
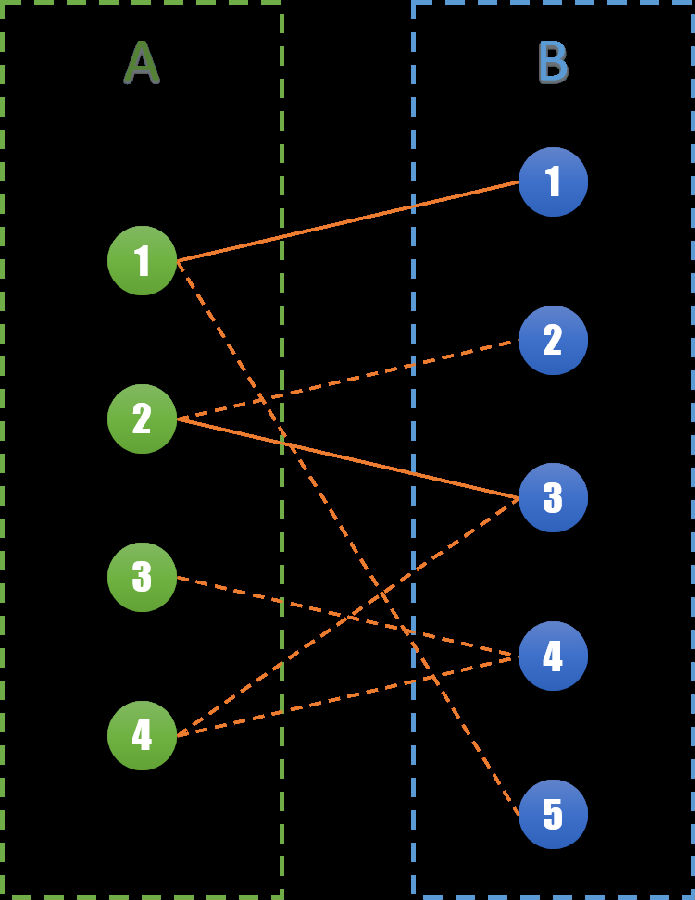



Hihocoder1122 二分图二 二分图最大匹配之匈牙利算法 太傅博客




二分图相关概念及匈牙利算法求解最大匹配 附代码实现 Codeantenna




二分图的最大匹配 匈牙利算法 简书
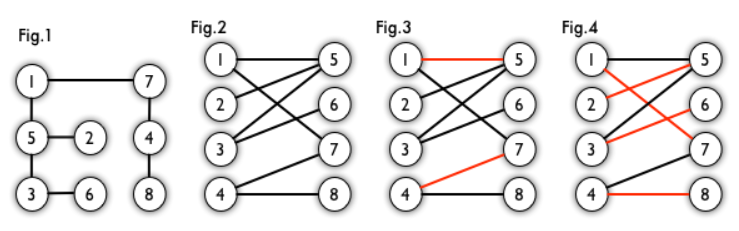



二分图的最大匹配 完美匹配和匈牙利算法 猪突猛进 博客园
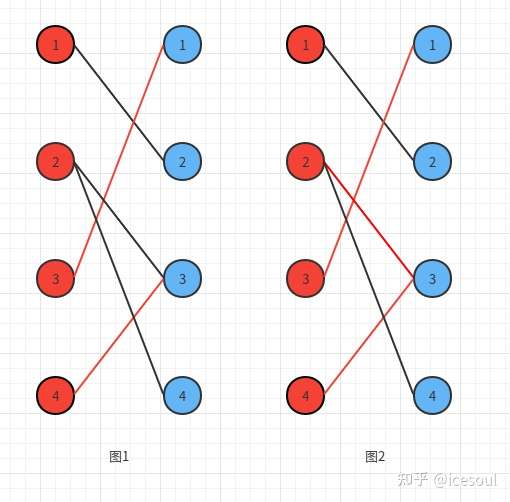



二分图与最大匹配 知乎




第5 1课 匈牙利算法与二分图的最大匹配 极思路



蒟蒻图论 二分图匹配 蒟蒻のblog




二分图最大匹配 匈牙利算法 海星的博客 Csdn博客




二分图 牛客博客




二分图最大匹配 最大流 Thinkspiritlab



二分图系列 二分图判定 匈牙利算法二分图的最大匹配 二分图最小点覆盖及最大独立集 Tham 博客园
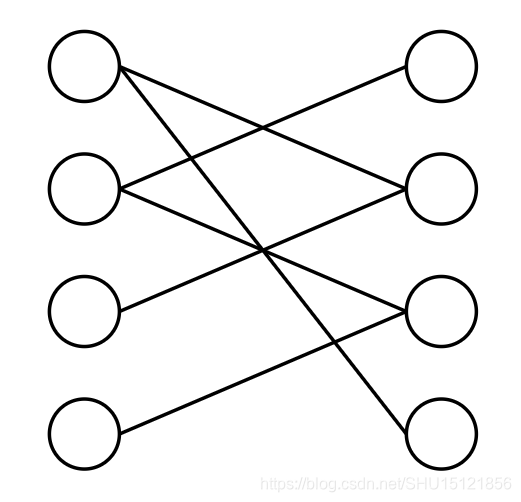



算法学习笔记 26 匈牙利算法 二分图最大匹配 Lauzyhou的笔记 Csdn博客



无权二分图的最大匹配求解 匈牙利算法求解 奋斗的程序猿的博客 Csdn博客



Oi 二分图最大匹配 Dudujerry 博客园




二分图匹配 搜狗百科



二分图最大匹配 最大流 忆南妄北的博客 程序员信息网 程序员信息网



算法 二分图最大匹配 Mina



算法学习笔记 5 匈牙利算法 知乎



通俗易懂小白入门 二分图最大匹配 匈牙利算法




二分图最大匹配算法



每日一侃 二分图最大匹配 匈牙利算法 Acwing



二分图的最大匹配问题 刘伟的博客 Csdn博客 最大匹配问题




算法导论 之 图 不带权二分图最大匹配 匈牙利算法 的技术博客 51cto博客



Acwing 基础 匈牙利解决二分图的最大匹配 码迷移动版 M Mamicode Com



蒟蒻图论 二分图匹配 蒟蒻のblog



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog




二分图的最大匹配算法简析 无道圣君 博客园



二分图匹配相关算法及例题分析最大匹配匈牙利算法最大权匹配km算法 二分图类型问题汇总 琳小羽 博客园
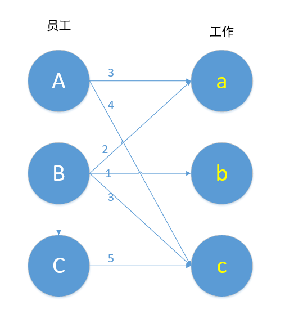



带权二分图匹配 Km算法 Ogmx的博客 Csdn博客 带权二分图



二分图的最大匹配 完美匹配和匈牙利算法 Yuanda S Blog




二分图匹配 匈牙利算法原理与实现 易学编程网
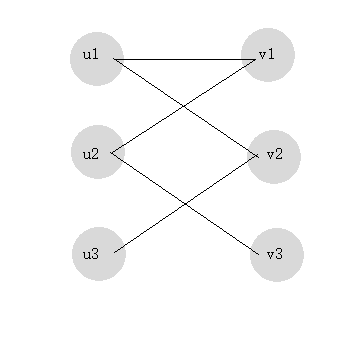



二分图匹配之最大匹配 匈牙利算法 Lanly 博客园




求解分配问题 二 二分图最大匹配算法 Wangzhenyang2的博客 Csdn博客
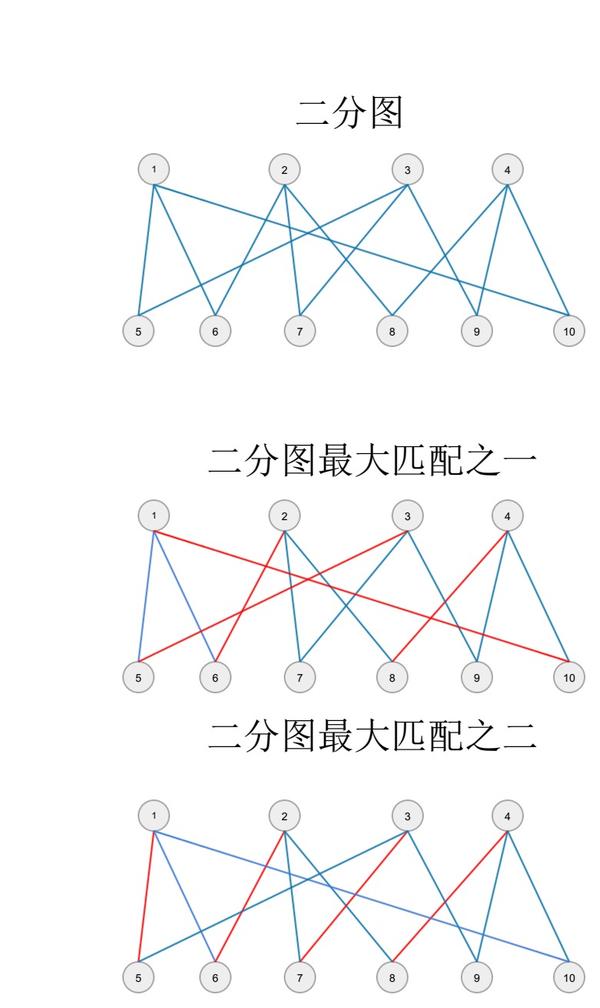



如何寻找一个二分图所有最大匹配 知乎用户的回答 知乎
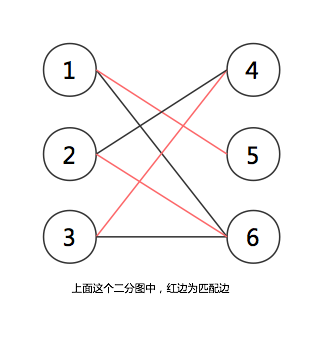



二分图 最大匹配 匈牙利算法 学习笔记 Tonyyin Blog
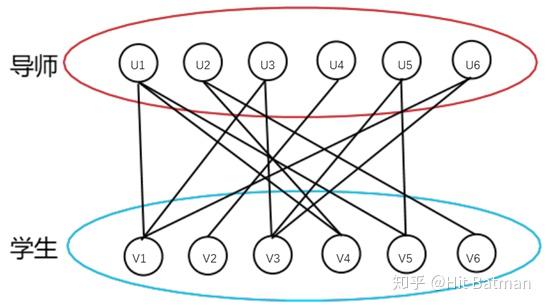



简单理解二分图与匈牙利算法 知乎



二分图最大匹配 第1页 要无忧健康图库




Learning 二分图最大匹配的konig定理



0 件のコメント:
コメントを投稿